
Diffraction is a manifestation of the wave nature of light. With the slit being completely open, however, the space between the slits (\(d\)) goes to zero, and the number of slits (\(n\)) goes to infinity. Diffraction is a spreading of light around the edges of obstacles.

One way to think of this is to go back to the diffraction grating case, expressed in Equation 3.3.2.

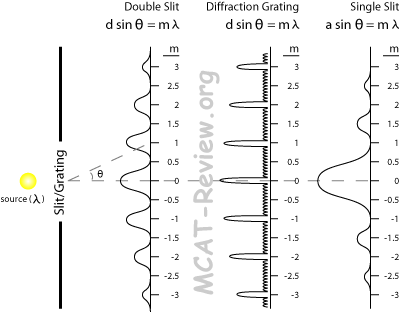
To compute the intensity of the interference pattern for a single slit, we treat every point in the slit as a source of an individual Huygens wavelet, and sum the contributions of all the waves coming out at an arbitrary angle. Significantly more math is required to deal with the intensity of the bright fringes. In water, for example, which has n 1.333, the range of visible wavelengths is (380 nm)/1.333 to (760 nm)/1.333, or n 285570 nm. It follows that the wavelength of light is smaller in any medium than it is in vacuum. The bright fringes only approximately follow the same spacing pattern, not exactly located halfway between the dark fringes, but using the pairwise approach doesn't tell us much about the intensity of those bright regions, for the same reason it didn't for the central bright fringe – constructive pairs will not be in phase with other constructive pairs. n n, where is the wavelength in vacuum and n is the medium’s index of refraction. Geometrical and Physical Optics (2nd ed.). Introduction to Fourier optics (3rd ed.). Principles of Optics: electromagnetic theory of propagation, interference and diffraction of light (7th ed.). Handbook of mathematical functions, with formulas, graphs, and mathematical tables. ^ Hecht 2002, p. 543, The array theorem.^ "Fraunhofer, Joseph von (1787-1826) - from Eric Weisstein's World of Scientific Biography".As the spread of wavelengths is increased, the number of "fringes" which can be observed is reduced. If the spread of wavelengths is significantly smaller than the mean wavelength, the individual patterns will vary very little in size, and so the basic diffraction will still appear with slightly reduced contrast. it consists of a range of different wavelengths, each wavelength is diffracted into a pattern of a slightly different size to its neighbours.

The first dark spot is at y 0.01 m just as it should be from the formula. In all of the above examples of Fraunhofer diffraction, the effect of increasing the wavelength of the illuminating light is to reduce the size of the diffraction structure, and conversely, when the wavelength is reduced, the size of the pattern increases. As expected, we see the classic diffraction intensity pattern from a single-slit. I ( x, y ) ∝ sinc 2 ( π W x λ R ) sinc 2 ( π H y λ R ) ∝ sinc 2 ( k W x 2 R ) sinc 2 ( k H y 2 R ) Non-monochromatic illumination


 0 kommentar(er)
0 kommentar(er)
